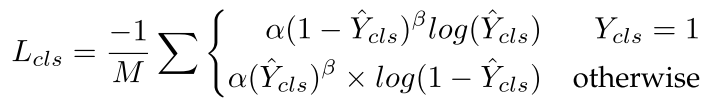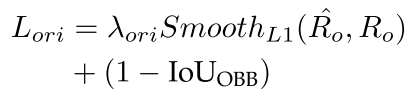
旋转目标检测 | IENet,单阶段Anchor-Free旋转目标检测模型
1. 论文信息
论文标题:《IENet: Interactive Embranchment Network Based One-Stage Anchor Free Detector for Orientational Aerial Object Detection》
论文发表:arxiv 2019
论文链接:https://arxiv.org/pdf/1912.00969
1 | @article{lin2019ienet, |
2. 归纳总结
| Name | Value |
|---|---|
| 标签 | #遥感 #目标检测 |
| 数据集 | DOTA,HRSC2016 |
| 目的 | 两阶段方法计算量大,单阶段方法性能不足 |
| 方法 | 基于自注意力的互动分支 |
3. 问题背景
作者提到,遥感图像的目标检测任务的难点在于:
- 和自然图像相比,物体形状相似且可见特征稀少
- 目标具有不同的旋转角度
- 具有更多的小目标和密集目标
而目前最好的性能都是两阶段算法实现的,但是两阶段算法通常在第一阶段定位,在第二阶段分类,因此计算量是非常大的,尤其是对旋转目标检测而言,因为Anchor匹配(涉及IoU计算)和RoI特征提取的计算量大。
4. 主要工作
针对上诉问题,作者提出了IENet(interactive embranchment network),其是一个单阶段的Anchor-Free旋转目标检测器,其包含如下贡献点:
- 一个新的geometric transformation(几何变换),用于更好地表示旋转目标框
- 一个基于自注意力机制的分支交互模块(a branch interactive module with a self-attention mechanism)
- 一个针对旋转框检测改进的IoU Loss
4.1 模型结构
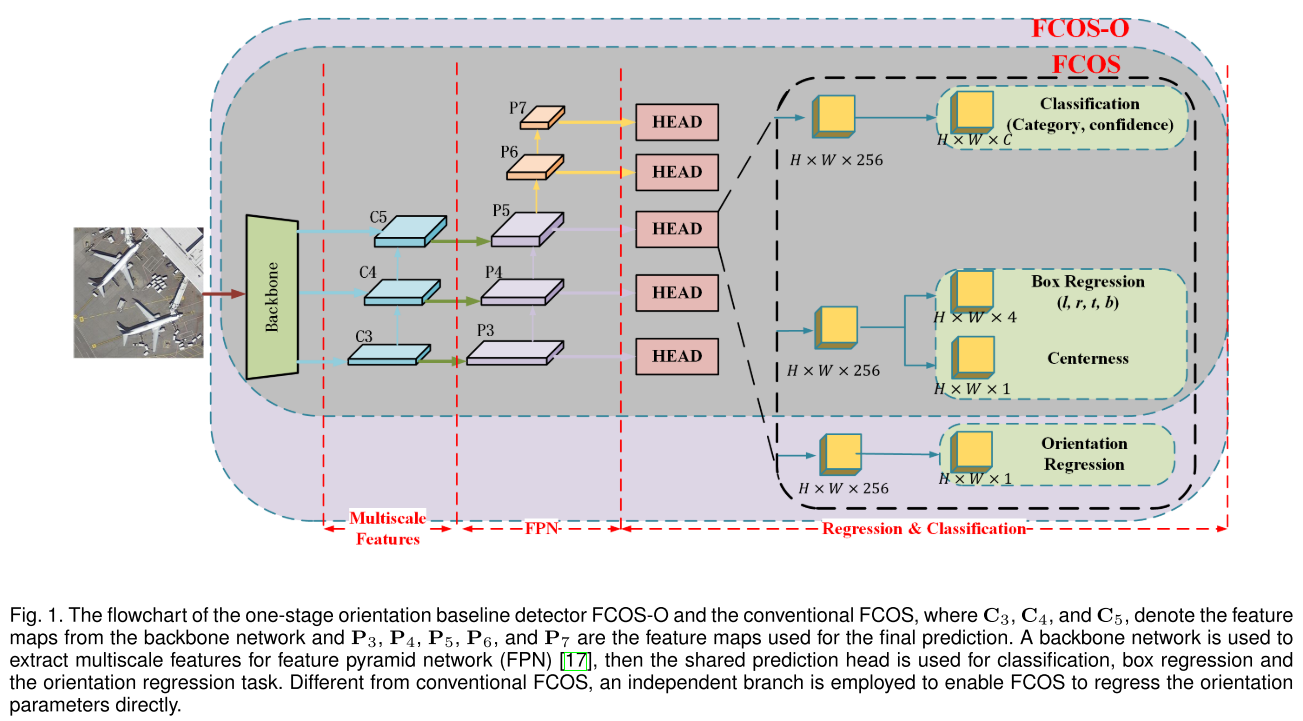
(1) Baseline模型结构(FCOS-O)
在FCOS的基础上增加了一个独立的角度回归分支(Orientation Regression)
(2) IENet
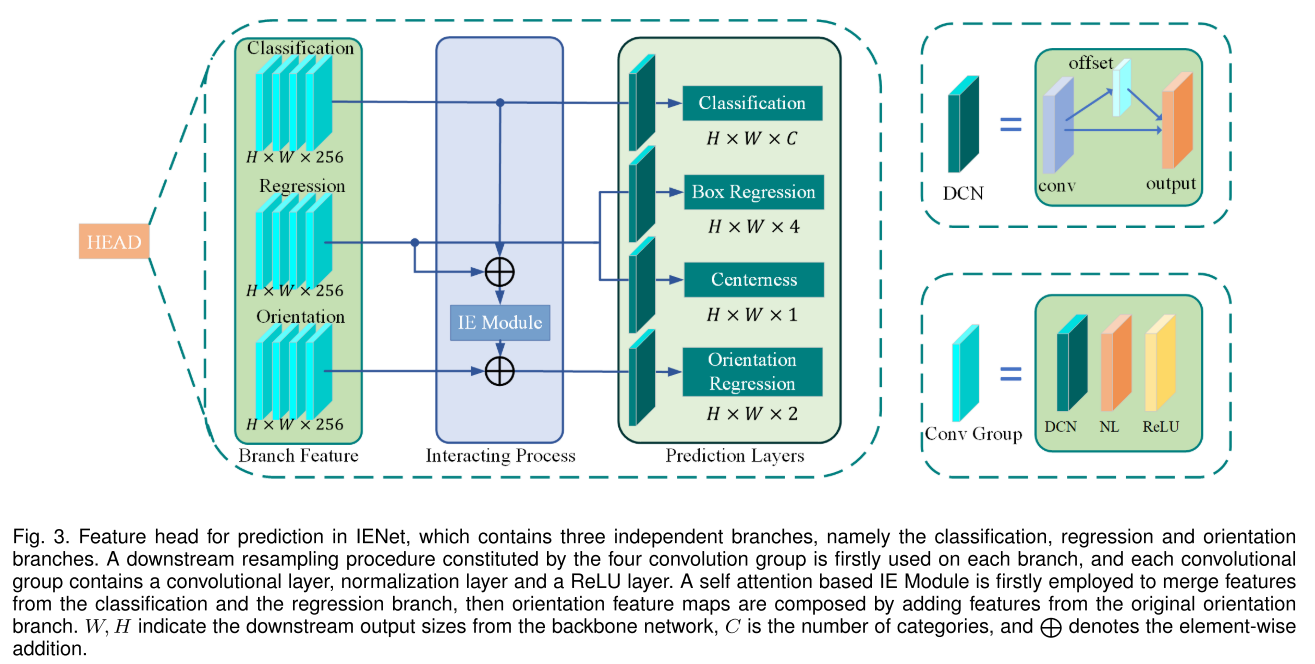
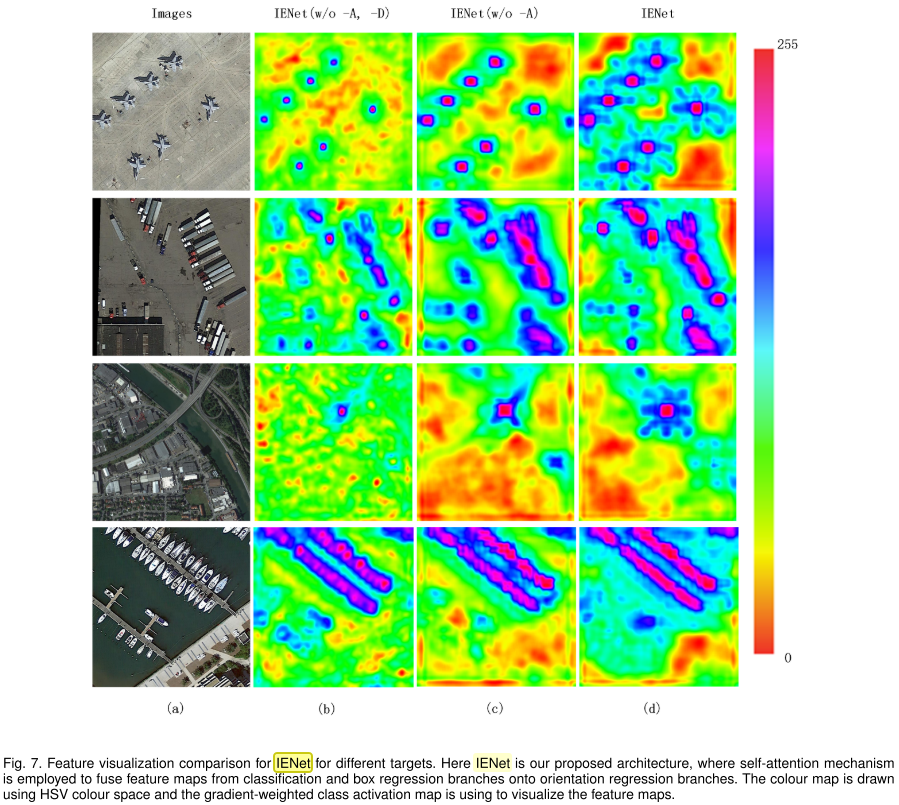
由于独立的角度分支不能很好的利用位置等信息,因此检测性能下降,基于此IENet提出了基于自注意力机制的分支交互模块即IE(Interactive Embranchment) Module,用于利用分类和位置回归信息。
4.2 旋转框几何变换
IENet使用HBB+几何变换来表征OBB,如下图所示:
IENet使用HBB加h,w来表示一个OBB,其中GT OBB是一个8维的向量$[x_1,y_1,x_2,y_2,x_3,y_3,x_4,y_4]$,HBB可由$[x_{min},y_{min},x_{max},y_{max}]$表示,h和w计算如下:
$$w=x_{max}-x_2$$
$$h=y_{max}-y_1$$
基于上述几何变化,可将OBB回归问题转换成HBB回归和方向回归的问题,其中HBB回归和FCOS的一致,为Box的偏移量$R_b=[l,t,r,b]$,方向回归为$R_o=[w,h]$.
4.3 IE Module
IE模块结构图:
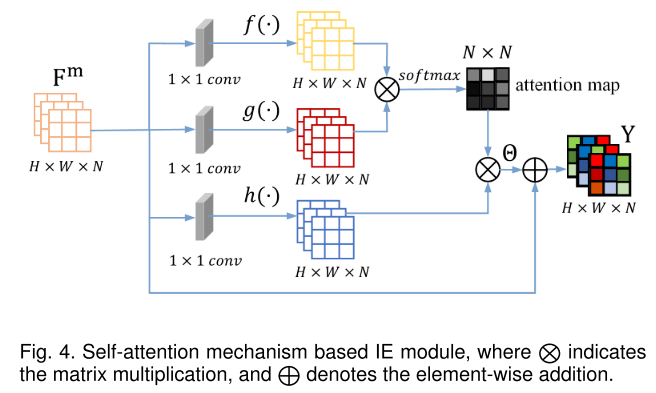
在获得了分类和位置回归的特征图$F^m$后,使用1x1的卷积层和softmax层来构建自注意力模块:
- 首先利用三个1x1的卷积层$f(F^m),g(F^m),h(F^m)$将特征映射到三个特征空间
- 将$f(\cdot)$和$g(\cdot)$和并通过softmax层组成注意力图$\gamma= softmax(f(F^m)^Tg(F^m))$,因此特征图之间的关系为$\gamma_{q,p}= \frac{exp(\delta_{pq})}{\sum_{p=1}^{N}exp(\delta_{pq})}$,其中$q,p\in{1,…,N}$为注意力图的行号和列号,$\delta$代表$f(F^m)^Tg(F^m)$输出的NxN的矩阵
- 然后,注意图可以用来表示输入特征之间的关系,并对$h(\cdot)$的起作用,得到$\theta=(\theta_1,\theta_2,…,\theta_1,…,\theta_N)$,且$\theta_q=\sum_{p=1}^N\gamma_{q,p}h(f_p^m)$
- 为了保留原始特征信息,最后输出的特征为$\mathbb{Y}=\gamma\theta+F^m$
4.4 损失函数
总损失为:
$$L = \frac{1}{N_{pos}}L_{cls}+\frac{\lambda}{N_pos}L_{reg}+\frac{\omega}{N_{pos}}L_{ori}$$
其中分类损失为Focal Loss损失
位置回归损失为centerness损失加smoothL1
角度回归损失为smoothL1损失
5. 实验结果
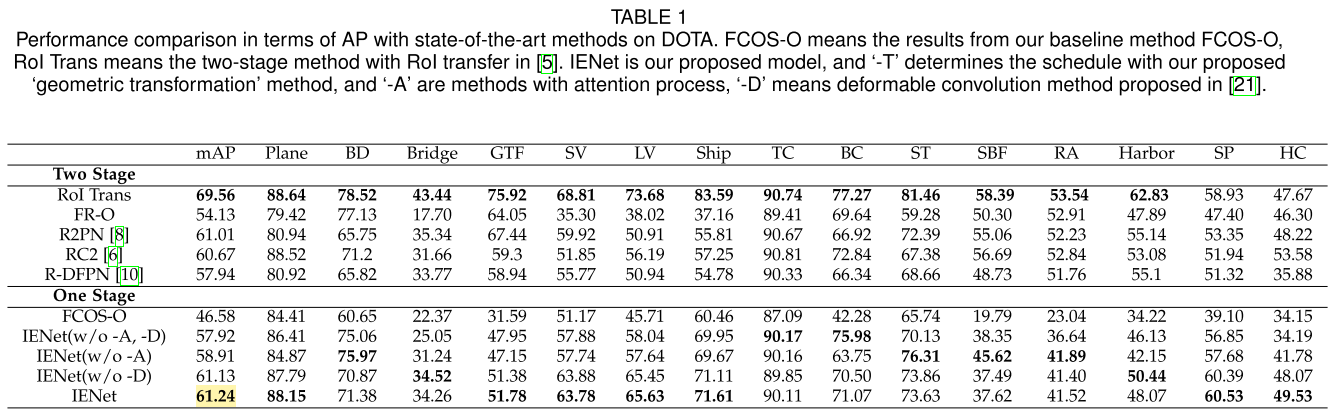
DOTA_v1
HRSC2016
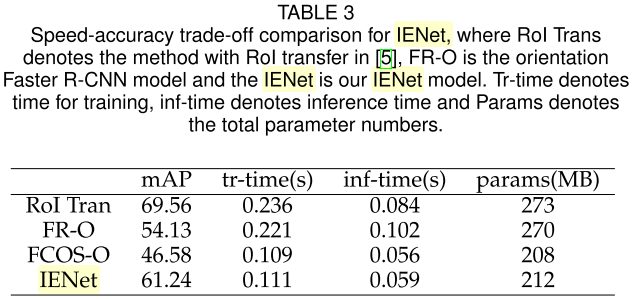
同时IENet在推理和训练时的速度上也有优势:
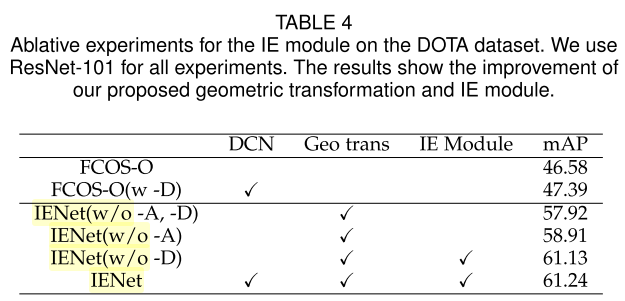
消融实验:
特征可视化: