1. 论文信息

论文标题：《Oriented RepPoints for Aerial Object Detection Wentong》

论文发表：CVPR2022
论文链接：http://openaccess.thecvf.com

@inproceedings{li2022oriented,
  title={Oriented reppoints for aerial object detection},
  author={Li, Wentong and Chen, Yijie and Hu, Kaixuan and Zhu, Jianke},
  booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
  pages={1829--1838},
  year={2022}
}

Name	Value
标签	#旋转目标检测 #标签分配
数据集	#DOTA #HRSC2016 #UCAS-AOD #DIOR-R
目的	设计面向航拍图像的旋转目标检测器
方法	基于RepPoint实现

2. 问题背景

作者提到航拍图像中目标具有非水平，任意方向，密集分布，背景复杂等困难，主流的方法大多将其视为简单的旋转目标检测问题。其中基于角度回归的方法最受欢迎，然而这种增加了角度预测的方法会面临损失的不连续性以及回归的不一致性问题。这是因为角度的有界周期性和旋转框的方向定义造成的。因此为了避免这种问题，一些方法重新定义了目标旋转框的表示方法。例如，基于点集表示的方法RepPoints可以捕获关键的语义特征。但是这种简单的转换函数只产生垂直-水平边界框，无法精确估计航拍图像中旋转物体的方位。同时RepPoint在忽略学到的点集的质量的同时只根据语义特征回归关键点集，会导致旋转的、密集分布的和复杂背景下的目标精度较差。

3. 主要工作

针对上述问题，作者提出Oriented RepPoints方法，其引入自适应点表示不同的方向，形状和姿势。同时该方法不仅可以精确定位任意方向目标，还可以捕获目标的底层几何结构。

文章贡献点如下：

提出了一个高效的航拍目标检测器Oriented RepPoint
提出了一个质量评估和样本选择机制用于自适应学习点集
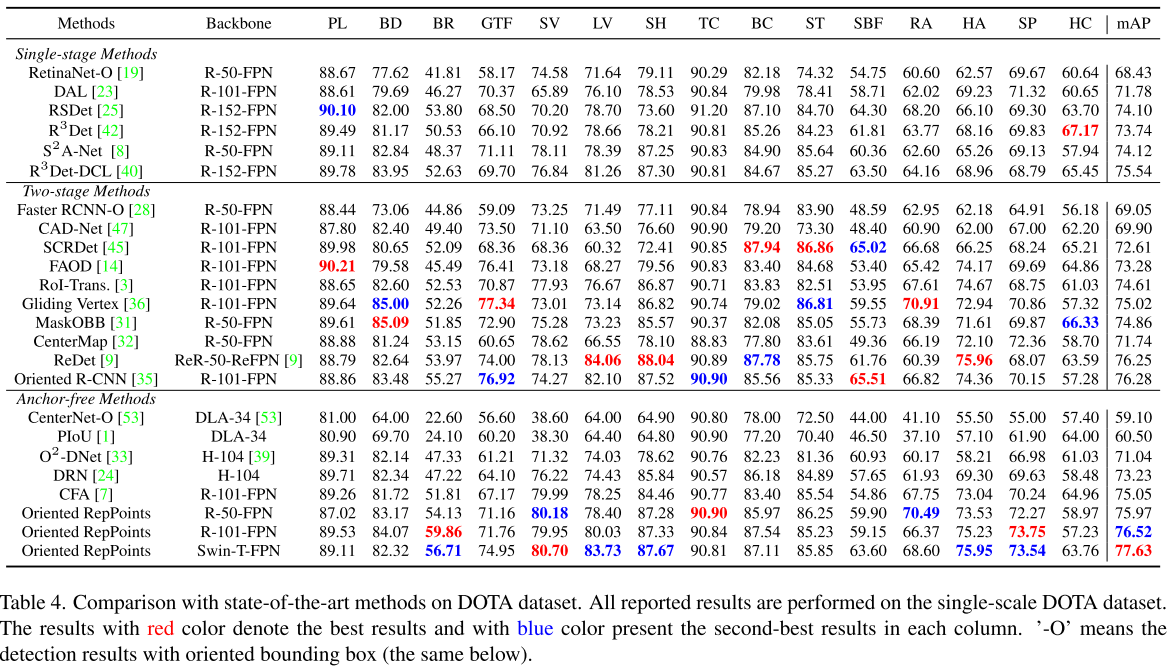
在四个具有挑战的数据集上实验并展现出不错的性能

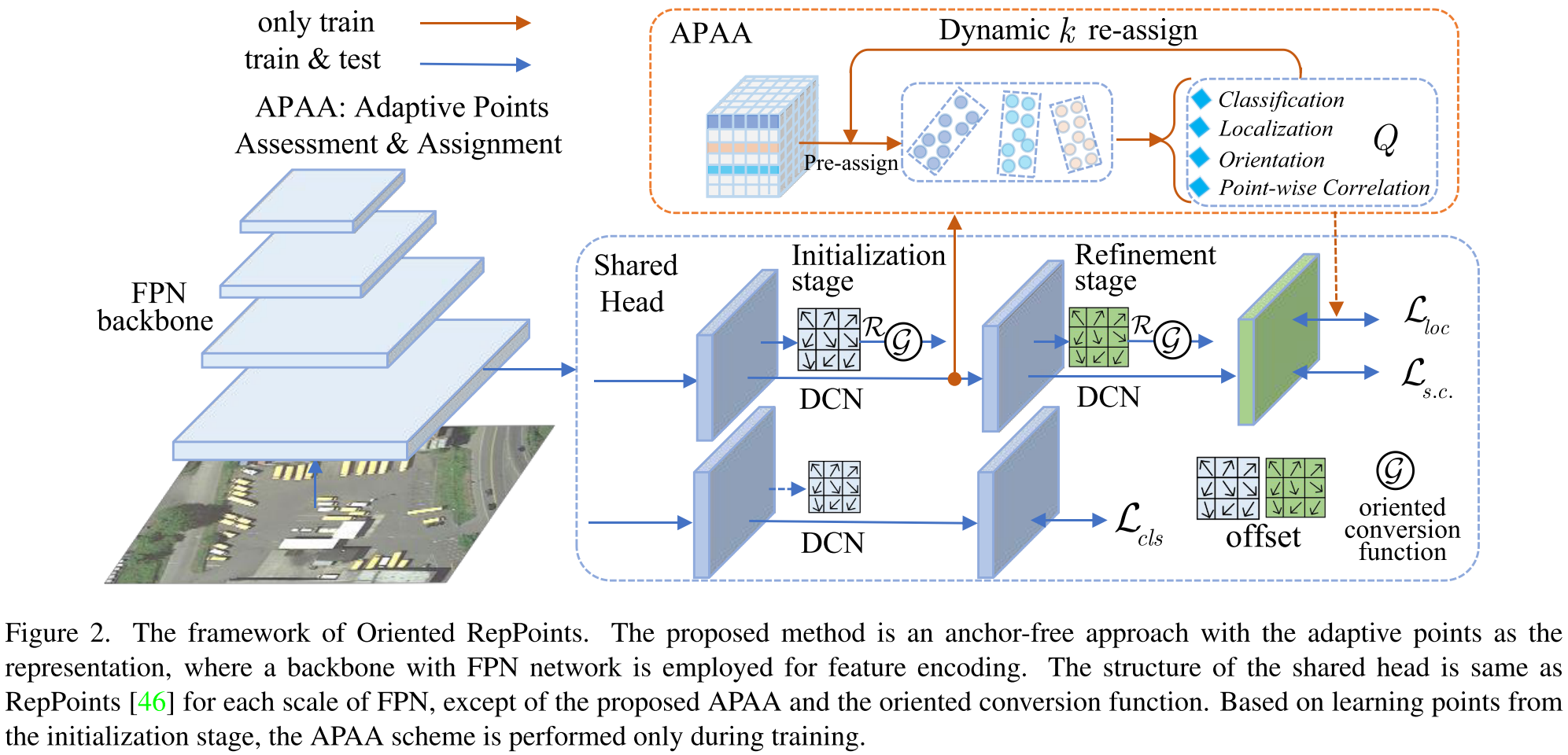
3.1 模型结构

与传统直接回归方向的方法不同，Oriented RepPoint利用自适应点集来细致地表征目标，甚至能够表征目标的几何结构。为了这个目的，Oriented RepPoint引入了可微分转换函数，其可以使点集自适应地移动到合适的位置。为了在没有直接点对点监督的情况下有效地学习高质量的自适应点，提出了一种在训练阶段选择高质量的方向点的质量度量策略。

3.2 自适应方位点集学习

为了将点集表示转换成旋转框表示，Oriented RepPoint引入了转换函数。在文章中，作者测试了三种转换函数，分别是：

MinAreaRect：点集的最小外接矩形构成边界框
NearestGTCorner：距离真值顶点最近的四个点构成边界框
ConvexHull：通过Jarvis March算法，从点集中取能包含所有点的最大凸四边形作为边界框

其中MinAreaRect不可微分，其他两个可微分，因此作者在推理时使用MinAreaRect，在训练时从NearestGTCorner和ConvexHull中任选一个。

Oriented RepPoint包含两个阶段，第一个阶段根据特征点生成自适应点集，第二个阶段为精炼阶段，对点集进行优化。损失函数如下：
$$L=L_{cls}+\lambda_1L_{s1}+\lambda_2L_{s2}$$
其中$\lambda_1,\lambda_2$是平衡权重，$L_{cls}$是分类损失：
$$L_{cls}=\frac{1}{N_{cls}}\sum\limits_iF_{cls}(R_i^{cls}(\theta),b_j^{cls})$$
其中$R_{i}^{cls}(\theta)$代表预测类别置信度，$b_j^{cls}$是真实类别，$F_{cls}$是focal loss。
$L_{s1},L_{s2}$分别代表第一阶段和第二阶段的空间定位损失，对于每一阶段定位损失计算为：
$$L_s=L_{loc}+L_{s.c.}$$
其中$L_{loc},L_{s.c.}$分别代表基于转换后边界框的定位损失（localization loss based on converted oriented boxes）和空间限制损失(spatial constraint loss)。其中
$$L_{loc}=\frac{1}{N_{loc}}\sum\limits_i[b_j^{cls}\geq1]F_{loc}(OB_i^{loc}(\theta),b_j^{cls})$$
其中$F_{loc}$代表GIoU损失，$N_{loc}$代表全部正样本点数。
$$L_{s.c.}=\frac{1}{N_a}\frac{1}{N_o}\sum\limits_{i=1}\sum\limits_{j=1}\rho_{ij}$$
其中$N_a,N_o$分别代表对每个目标分配的正样本点数以及在真值框外的点数。
$$\rho=\begin{equation}
\begin{cases}
||p_o-p_c|| , & \text{$p_{o}$ is outside GT} \
0 , & \text{otherwise}
\end{cases}
\end{equation}
$$
其中$p_o$代表GT外的点，$p_c$代表GT的中心点

3.3 APAA

首先，APAA定义了一个质量评估值Q，该值从四个方法来度量学到的自适应点集的质量。
$$Q=Q_{cls}+\mu_1Q_{loc}+\mu_2Q_{ori}+\mu_3Q_{poc}$$
其中$Q_{cls},Q_{loc},Q_{ori},Q_{poc}$分别代表分类置信度（classification confidence），空间位置距离（spatial location distance），Chamfer距离（Chamfer distance）以及特征多样性（point-wise feature diversity）。Chamfe距离计算如下：
$$CD(R^v,R^g)=\frac{1}{2n}\sum_{i=1}^nmin_{j}||(x_i^v,y_j^v)-(x_i^g,y_j^g)||2+\frac{1}{2n}\sum{j=1}^nmin_{i}||(x_i^v,y_j^v)-(x_i^g,y_j^g)||2$$
特征多样性计算如下：
$$Q{poc}=1-\frac{1}{N_p}\sum_{k}cos<e^\star_{i,k},e^\star_i>=1-\frac{1}{N_p}\sum_k\frac{e^\star_{i,k}\cdot{e^\star_i}}{||e^\star_{i,k}||\times||e^\star_i||}$$
之后针对每个目标，利用Q值，选择前k个样本作为正样本。