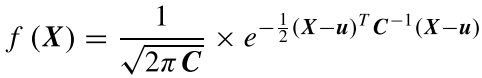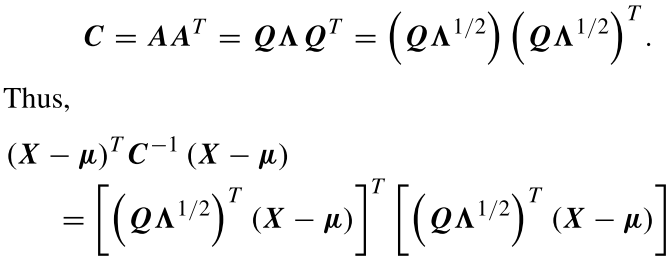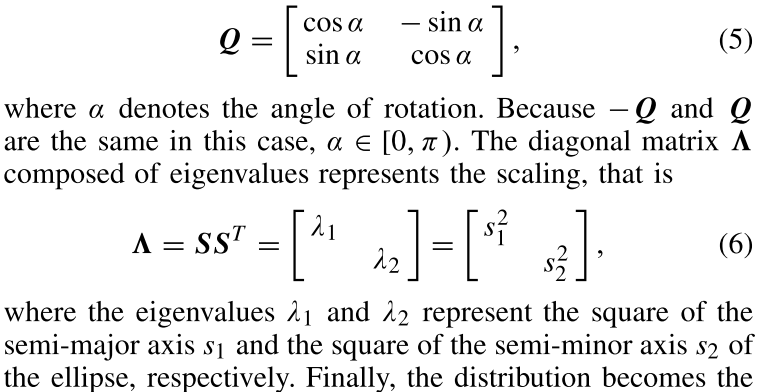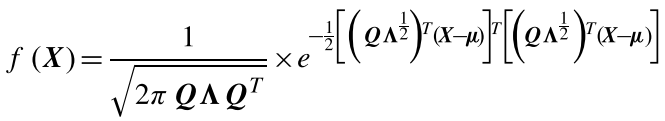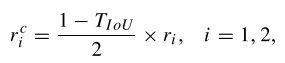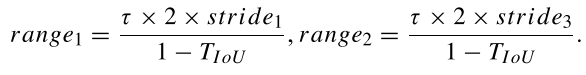标签分配 | GGHL,面向旋转目标检测的标签分配策略
1. 论文信息
论文标题:《A General Gaussian Heatmap Label Assignment for Arbitrary-Oriented Object Detection》
论文发表:2022 IEEE TRANSACTIONS ON IMAGE PROCESSING
论文链接:https://ieeexplore.ieee.org/document/9709203
1 | @article{huang2022general, |
| Name | Value |
|---|---|
| 标签 | #遥感 #标签分配 #旋转目标检测 |
| 数据集 | #DOTA #DOTAv2 #SKU10-R #SSDD |
| 目的 | 解决旋转目标检测任务中,采样策略没有考虑目标的形状和方向特性的问题。 |
| 方法 | 提出了GGHL,其包含OLA,ORC以及JOL |
2. 问题背景
作者提到近年来,大多数做旋转目标检测的方法都是设计复杂的网络结构以使得提取的特征分布接近GT的分布。然而改进模型结构不是提升性能的唯一解决途径。下图可见,一个完整的检测流程包括:数据;标签分配(正负样本划分);模型结构;目标函数(损失)。
对于CNN-Based检测器而言,如何提升标签分配也很重要,不同的策略将会通过影响生成的样本空间来直接影响模型的性能。因此,要想提升检测性能,一个方法是使用复杂的CNN结构(复杂的近似估计函数),另一个方法是设计标签分配策略从而构建更好的能够反映目标特性的样本空间。
目前一些工作采用的标签分配策略如下:
(1)Anchor-Based Label Assignment
SCRDet,LO-Det,DAL,CenterMap,DCL以及Oriented R-CNN等使用的基于Anchor的标签分配策略。(计算IoU,通过和阈值比较来判断)这种方法会导致正负样本误分。
(2)Dense-Points Assignment
FCOS,IENet,AOPG等使用更宽松的采样策略,会导致样本空间中混入负样本。
(3)Key-Point Assignment
CenterNet,BBAVector以及O2DNet等使用更严格的采样策略,导致正负样本严重不平衡。
因此一个上述标签分配策略都没有考虑目标的旋转和形状特性,故而存在很多不足。此外,即便得到了更好的训练样本空间,还需要一个合适的目标函数来引导模型学到更高质量的特征。而目前,主流的目标函数都是独立优化分类和回归分支。因此其可能导致精准定位的预测框只有很低的分类得分,或者高得分的目标定位不准。因此,PISA,Free-Anchor,以及AutoAssign等方法将不同子任务联合训练来实现更理想的性能。
3. 主要工作
针对上述问题,作者提出了通用高斯热力图标签分配策略(GGHL),其主要包括三个部分:
- 一个目标自适应的采样策略(OLA),基于2D旋转高斯热力图,使得采样策略更能反映目标的尺寸和方向特性。
- 一个旋转边界框表示组件(ORC),基于正样本点到OBB顶点的距离构建OBB的表示方法。此外,还使用了一个目标自适应加权调整机制(OWAM),用于自适应调整不同位置的高斯中心权重以加权不同位置的损失。
- 一个带有面积归一化和动态加权的联合优化损失(JOL),用于精炼正负样本间未对齐的优化目标,并可以平衡模型对于不同位置不同大小的不同类别的目标的学习能力。
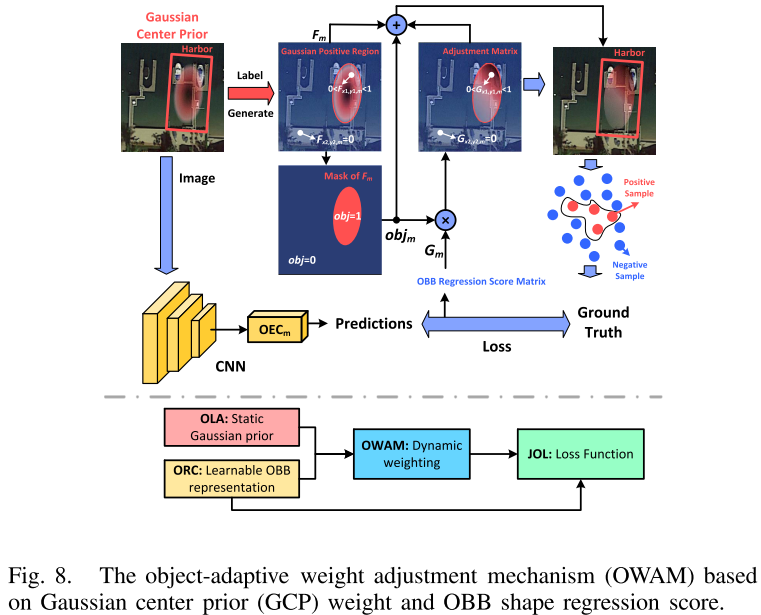
3.1 模型结构
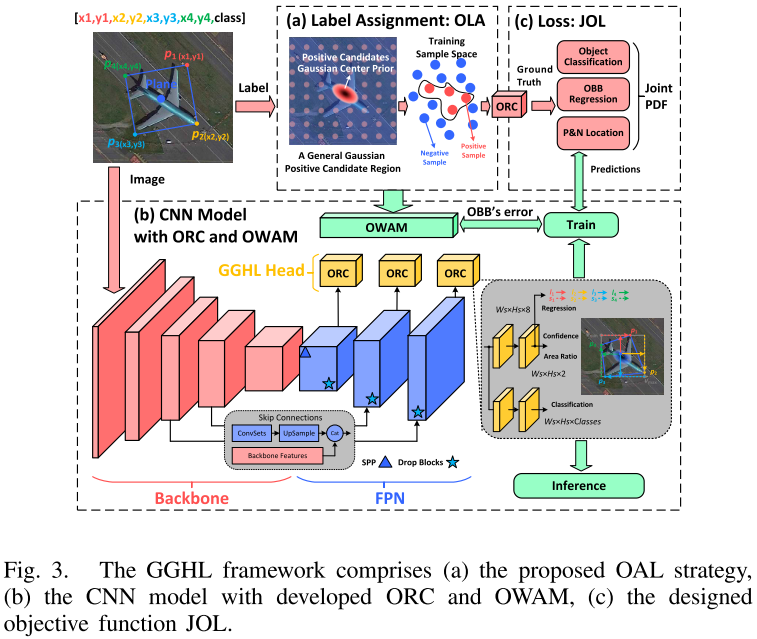
下图为GGHL的结构框架。
3.2 目标自适应采样策略(OLA)
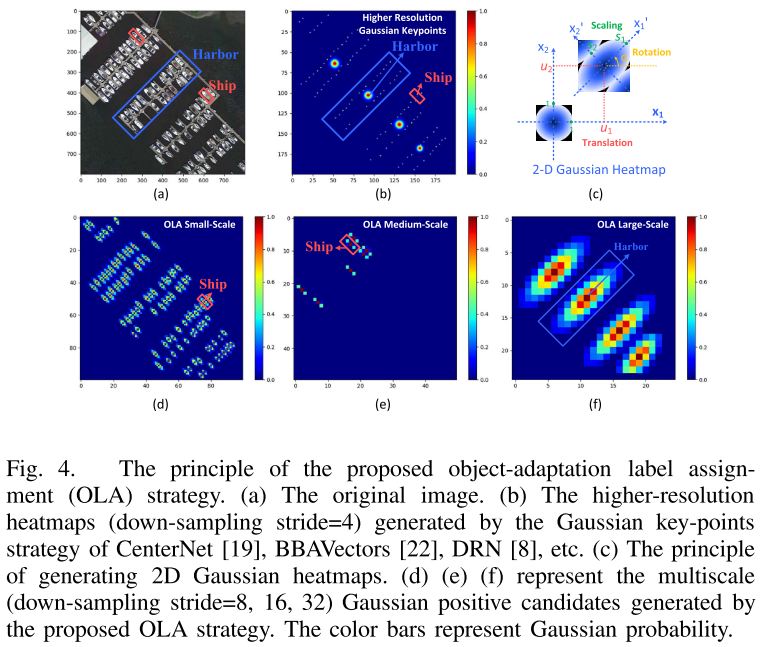
作者提到,之前的标签分配(Label Assignment,LA)存在样本误匹配的问题,并且存在大量超参数。如GWD使用2D高斯来计算损失,其LA仍基于Anchor实现。CenterNet,BBAvector,DRN等使用标准高斯分布(圆形)不能反映目标的形状和方向特性,并且其只使用高斯峰值点作为正样本加剧了正负样本不平衡,并且使用高分辨率特征图加大了计算复杂性。因此作者提出的OLA采用旋转椭圆高斯区域来采样。
(1)与标准高斯分布不同,OLA使用整个高斯区域作为正样本采样区域,再根据高斯密度函数对不同位置加权。高斯概率密度函数如下:
其中$X=[x,y]^T\sim N(\mu,C)$,$\mu\in R^2$代表平均向量,$C\in R^{2\times2}$为非负半定实矩阵,代表两个变量的协方差矩阵。实对称矩阵$C$正交对角分解为:
其中Q为实对称矩阵,$\Lambda$代表由降序特征值组成的对角矩阵。
高斯概率密度函数变换为:
如果$f(x,y)>0$,该位置定义为正样本,且其值代表该位置的权重。
(2)对于重叠问题,如果一个位置包含在不同的高斯区域内,则将其分配给$f(x,y)$最大的那个高斯区域。
(3)空间和尺度范围。对于空间范围,设高斯峰值的边界框为C-BBox,此时其他位置的边界框与C-BBox的IoU大于阈值$T_{IoU}$则视为正位置(positive location)。这些正位置构成了原始高斯候选区域的一个子集(表现为一个较小的椭圆,与原始高斯椭圆共心),其半轴长度为:
其中$r_i$代表原始高斯椭圆的半轴长度。
而对于尺度范围,假设不同特征层的下采样率为$stride_m=2^{m+3},m=1,2,3$,同时为了保证在空间尺度上正样本的数量,定义$max_i(r_i^c)/stride_m\geq 1$,即$max_i(2r_i)\geq \frac{2\times stride_m}{1-T_{IoU}}$。定义OBB的四条边长为$d_j,j=1,2,3,4$,则有$max_j(d_j)=max_i(2r_i)\geq \frac{2\times stride_m}{1-T_{IoU}}$。定义一个超参数$\tau=3$,得到两个阈值:
此时,当$max_j(d_j)\in (1,range_1)$时,目标分配给$stride_1$。当$max_j(d_j)\in(range_1,range_2]$时,目标分配给$stride_2$。当$max_j(d_j)\in(range_2,\sqrt{2}len^{img}]$时,目标分配给$stride_3$。
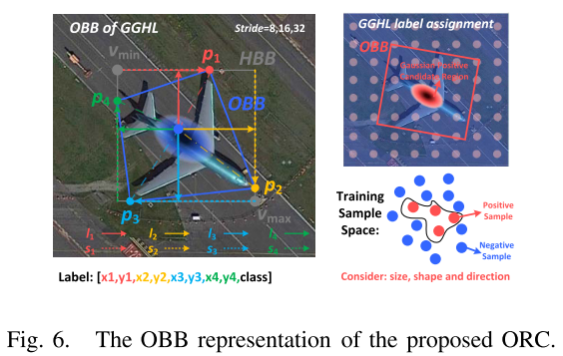
3.3 旋转边界框表示组件(ORC)
作者提到,现有的OBB表示方法有两类,一类是基于角度的,如CenterMap,另一类是基于点的,如Gliding Vertex。ORC如下图,使用$l_{x,y,m}=[l_1,l_2,l_3,l_4]$以及$s_{x,y,m}=[s_1,s_2,s_3,s_4]$来表示一个位于$(x,y) _ {m}$的点所表示的OBB。其中与Gliding Vertex一样,使用$ar_{x,y,m}\in[0,1]$表示HBB和OBB的面积比例,因此ORC相当于使用一个9维的向量表示OBB:$obb_{x,y,m}=[l_{x,y,m},s_{x,y,m},ar_{x,y,m}]$。
除此之外,并不是每一个凸四边形都能被ORC表示,还需要讨论顶点不在HBB上的情况以及ORC中顶点的隐式排序。
此外,直接使用高斯分布来加权并不适合部分目标,如港口等等。因此需要设计一种自适应的加权调整策略,如AutoAssign以及IQDet等等。因此借鉴此思想,作者提出了OWAM。
3.4 联合优化损失(JOL)
包括:
- 联合概率密度函数
- 面积归一化和损失重加权机制
- 用于实现整个联合优化函数的极大似然估计
4. 实验结果
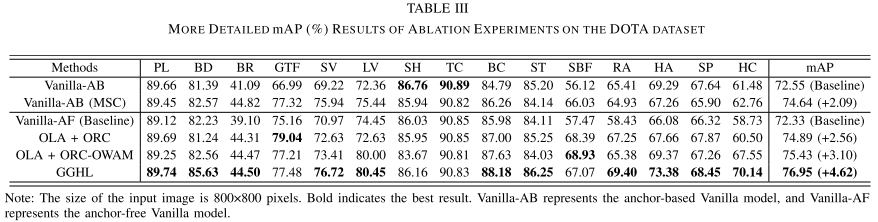
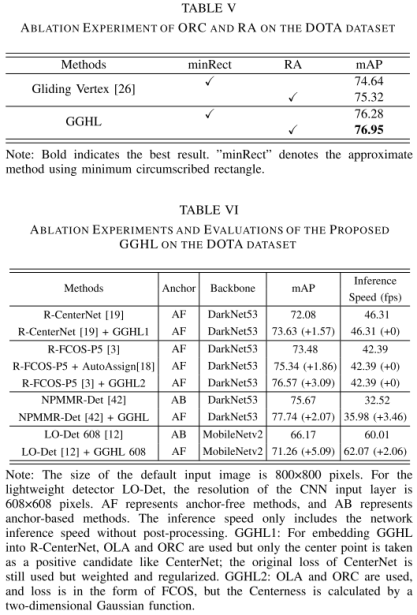
(1)消融实验
(2)可视化结果
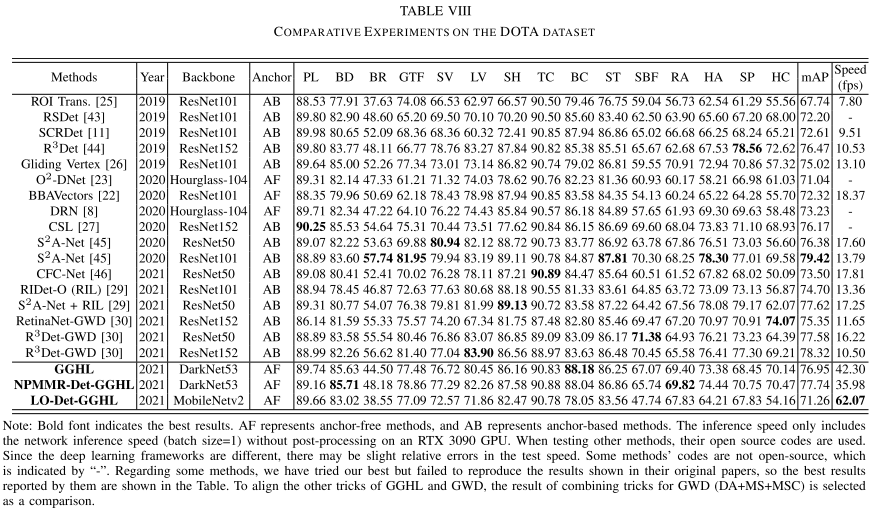
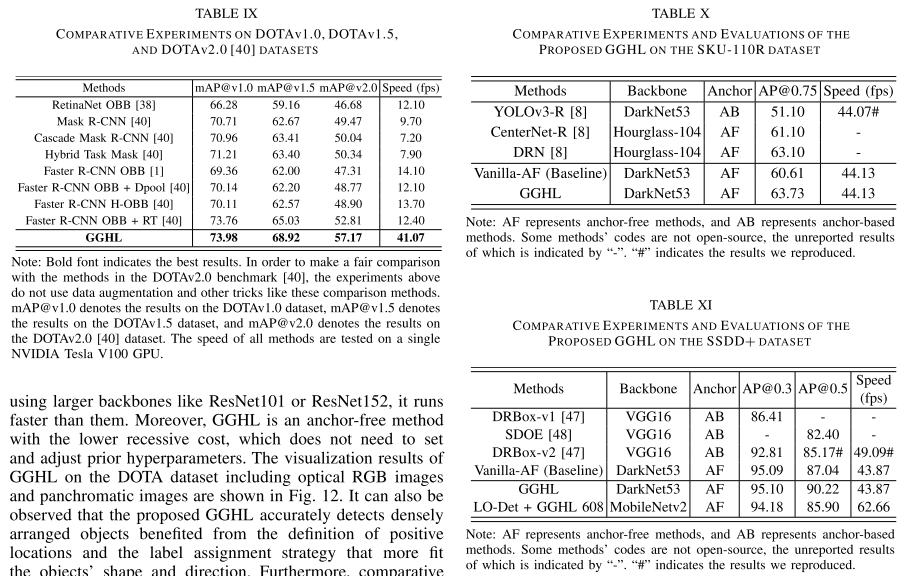
(3)对比实验